信息的二进制编码

什么是信息?
- Infotmation is a message that is previously uncertain to receivers
怎么表示信息?
- Codebook (Dictionary)
怎么度量信息?
- 朴素的做法: 度量码长
  - 前提: 没有歧义表达 (如: A-0 B-1 C-10 若要表达10, 既有BA又有C,发生歧义)
  - 累加上(每个字符出现的概率 * 该字符所拥有的比特数)
- 三个公设
  - Monotonicity in event probability: 事件所发生的概率作为度量的标准
  - Additivity: 两个独立事件发生概率可加
  - Continuity
- 自信息量: I(x_i) = -log₂p(x_i)
- 一个系统的信息熵
在冯诺依曼结构中, 所有信息 (代码和数据) 都采用二进制编码
- 编码: 用少量简单的基本符号对复杂多样的信息进行一定规律的组合
- 采用二进制的原因
  - 制造两个稳定态的物理器件容易
  - 二进制编码和计数运行规则简单
  - 对应逻辑命题中的"真"和"假"
  - 便于使用逻辑电路实现算术运算
- 真值和机器数
  - K位的二进制编码至多表示**2^k**个不同的值

整数的二进制数表示

优点: 最直接, 便于理解
缺点:
- 0的表示不唯一, 不利于程序员编程
- 加减运算方式不统一, 尤其当a<b时, 实现a-b比较困难
- 需要额外对符号位进行处理, 不利于硬件设计

-1.01 * 2²⁰
- 符号: -
- 尾数: 1.01
- 基/底: 2
- 阶/指数: 20
规格化表示
- ±1.bbb … b * 2^E
- X = (-1)^S * M * 2^E
- E使用移码: 例如计算1.01 * 2^-1 + 1.11 * 2³时, 须要将低阶 (2^-1) 转成高阶 (2³), 那么首先需要比较-1和3的大小
- M使用原码: 对称, 无符号时原码的乘法运算简单
  
  S E M
  
  1位 8位移码 23位原码表示24位尾数 (因为第一位永远是1)
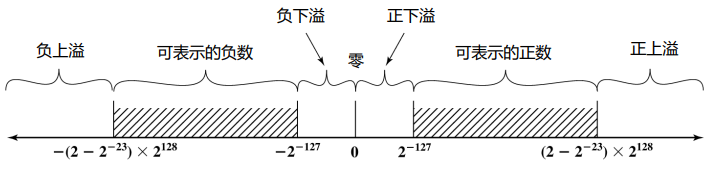
- 最大正数: (2 - 2^-23) * 2¹²⁸ 因为1.11…11 = 1 + 0.11…11 = 1 + (1 - 0.00…01) = 2 - 2^-23
- 最小正数: 2^-127 E = 0, M = 0
- 对一定长度 (总位数不变) 的规格化数, 表示范围和精度之间存在权衡问题
  - 增加阶码 (E) 位数: 扩大表示范围, 降低表示精度
  - 增加尾数 (M) 位数: 减少表示范围, 提高表示精度
  - 更大的底 (B) 位数: 扩大表示范围, 降低表示精度
- 值的范围
IEEE 754 标准
- 32位单精度
  
  S E M
  
  1位符号位 8位移码 23位有效值
- 64位双精度
  - S E M
    
    1位符号位 11位移码 52位有效值
- E: 全0和全1表示特殊值, 范围是 0000 0001 (-126) ~ 1111 1110 (127)
- 值的范围:
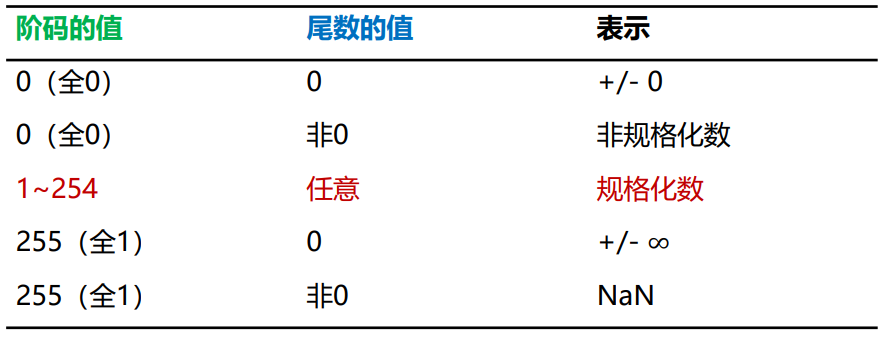
- 全0和全1
  - 用于表示格式化数以外的情况
  - 负上溢和正上溢只能表示无穷